QCD theory at high energies and nonzero temperatures

Quantum chromodynamics (QCD) is a core ingredient of the Standard Model of Particle Physics, with its relatively short list of elementary constituents of matter and force carriers, all wrapped in an short elegant mathematical framework.

QCD, also referred to as the theory of the strong force, describes the force that binds quarks into their known bound states, the objects that constitute all directly observable matter, predominantly protons and neutrons. Its force carrier, the gluon is the preeminent channel for particle production in modern high energy collider experiments such as the LHC at CERN.

QCD is a complicated theory with many emergent features, faces that surface in ways strongly depending on the expermental circumstances: unlike gravity or electromagnetism, the force becomes weaker at short distances (or if probed at high resolutions), a phenomenon know as asymptotic freedom. This is naturally complemented by another feature not shared by the other forces in the standard model: confinement of quarks (and gluons): one can never observe an isolated quark (or gluon) since the force between any two (or more) of them does not fall of with distance. Instead, the energy required to pull quark away from a bound state keeps increasing with distance to the remnants and will eventually reach the threshold for the production of a new quark-antiquark pair, resulting in a new pair of bound bound states, not an isolated quark and a “remnant”. The only option to see a macroscopic state of quasi free quarks and gluon is a situation in which, in a large enough volume, the temperature and density is large enough to sustain free movement over volumes larger that the proton size, i.e. by driving the system beyond a phase transition into a phase known as the Quark Gluon Plasma (QGP). If we go far enough back in the evolution of the universe to about a microsecond after the big bang, this is, in fact, the state of matter permeating the whole universe.

 

 

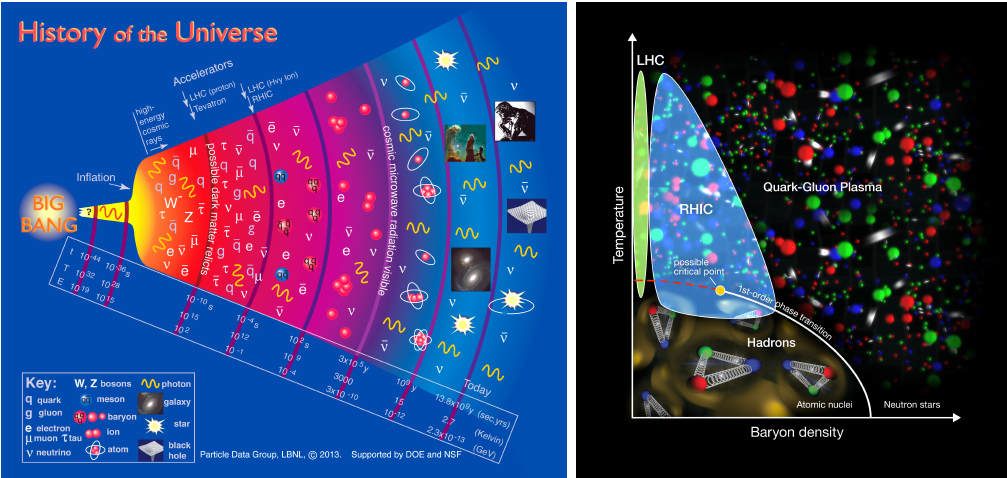
Left: History and size of the universe from the big bang to today. Several phase transitions occur before matter and light decouple and the universe becomes observable by astronomical means after the cosmic microwave background is created. Right: Phase transitions in the early universe can be triggered by high temperatures and densities. Modern collider experiments explore these conditions for the first time since the big bang. (The universe followed a trajectory from top to bottom, very near the temperature axis through the region probed by LHC) (Sources: left: Particle Data Group, right: BNL, STAR collaboration)

Modern collider experiments like the LHC at CERN or RHIC at BNL are able to recreate this state of matter (each with slightly different parameters, see Fig. 4) and tell us about a state of matter dominating an era of cosmic evolution hidden behind the cosmic microwave background (the earliest cosmological feature observable by astronomical means). To recreate this state experimentally, RHIC and the LHC, create temperatures in excess of a 100 000 times the temperatures at the center of the sun: This truly are the hottest spots in our universe today – no matter how short lived and how tiny. The nature of these experiments is by necessity complicated: Both the initial state and the final state must consist of ordinary matter: bound states of quarks and gluons known as hadrons. Only a short intermediate time is governed by a quark gluon plasma in a highly dynamic expanding environment at best in local thermal equilibrium.

 

 

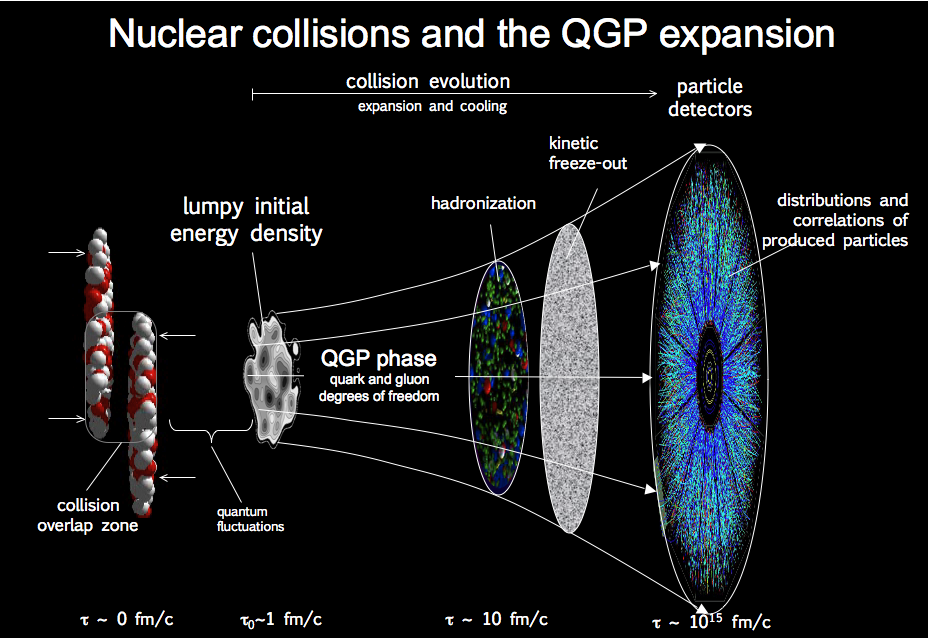
Time evolution in a heavy ion experiment: From left to right: 1) two heavy ions collide headon, strongly influenced by relativistic effects (Lorentz contraction), 2) An high energy density is created in an irregular volume, 3) A QGP is formed for a very short time, cools and expands 4) hadrons (bound states of quarks are formed that further interact 5) The final state particles are separated far enough thatfurther interaction ceases (freeze out) and 6) reach the detector. (Graphics by Paul Sorensen.)

Moreover, to deposit enough energy in a large enough volume, the initial states are not the relatively simple protons, but instead the largest manageable ions at our disposal, typically gold or lead. The high energies involved lead to an immensely crowded final state which pose enormous experimental challenges.

Theory faces a long list of complementary challenges:

• The initial states are highly modified by the high energies involved in the collisions: this is a feature of QCD as a quantum field theory – the properties probed in an experiment depend strongly on the experimental conditions, a general phenomenon for which particle wave duality is but one example. The tools to describe these initial sate are provided by the Jalilian-Marian Iancu McLerran Weigert Leonidov Kovner equation (JIMWLK for short) and play a vital role in the subsequent stages of the collision.
• It is known that the system reaches (local) thermal equilibrium and can be described by hydrodynamics. The time scales for this equlibration are so short that simple single particle interactions can not explain this observation. One of the main experimental observation thus remains without a theoretical explanation. There are different attempts to think about this, some aiming to employ resummation techniques for QCD at weak coupling, others utilize strong coupling techniques based on string theory, both based on JIMWLK initial states. The QCD approach relies on a proper treatment of collective effects and instabilities, while the strong coupling approach references the string motivated AdS/CFT correspondence to step beyond a naive treatment of equilibration, encouraged by experimental results that place the QGP viscosity near the lower bound present in AdS/CFT models.
• The thermal properties of heavy ion collision and the precise value of the phase transition temperature, the critical temperature of QCD remain an important issue and numerical tools to analyze experimental results remain at a premium, THERMOS, a computer code developed at UCT is in heavy use for this purpose.
• As the system expands, cools down and hadronizes, it crosses the critical temperature once more, now in a somewhat more gentle manner. Here a good understanding of the QCD phase transition becomes essential. Ab initio QCD simulations (not done at UCT) provide a good quantitative understanding, but limited conceptual insight. A set of techniques known as QCD finite temperature sum rules can provide insight here and be linked with effective field theory techniques to provide a further angle of attack.

Cosmology

To quote from wikipedia: “Cosmology is the science of the origin and development of the universe. Modern cosmology is dominated by the Big Bang theory, which brings together observational astronomy and particle physics”. In this panorama, particle physics is most directly concerned with the steps before the creation of the microwave background , steps that set the stage for all further development. Direct observation is limited to the time after that, and thus biases a focus on those later times, with questions like large scale structure formation, gravitational properties of galaxies and signals travelling long distances through space time. These seemingly purely astronomical questions raise important issues that again challenge particle and string theorists with the existence of dark matter and dark energy

• Dark matter: Evidence comes from velocity profiles of galaxies, gravitational lensing observations and traces in the microwave background.
• Dark energy: Observations of remote supernovae prove that the expansion of the universe is accelerating, which can only be explained by an effect that counteracts gravitational attraction – dark energy.

Both phenomena have no satisfactory explanation either in particle physics or string theory at this point, although strong efforts are underway, with dark matter candidates often looked for in super-symmetric extensions of the standard model of particle physics, and dark energy candidates like chameleon particles being actively searched for in particle physics experiments. Cosmology itself is progressing into a phase of precision cosmology in which relativistic corrections to lensing effects start to become important and will influcence precision details of what is known as the standard model of cosmology, new experiments like the SKA will harvest unprecedented amounts of new
data that will challenge our view of the universe once more.

Mathematical Physics: Nonlinearity with PT-symmetry

Our current activities focus on nonlinear systems with parity-time symmetry. We study properties of finite-dimensional PT-symmetric models (canonical formulations, integrability, self-trapping, PT-symmetry breaking and blow-up phenomena). We are also interested in localized structures (solitons, breathers and vortices) supported by infinitely-dimensional PT-symmetric systems. This mathematical research is driven by the current wave of enthusiasm in photonics where the unidirectional light propagation in PT-symmetric materials raises hopes for the design of invisible cloaks and similar unprecedented optical behavior.

Nonlinear Dynamics: Solitons and Patterns

 

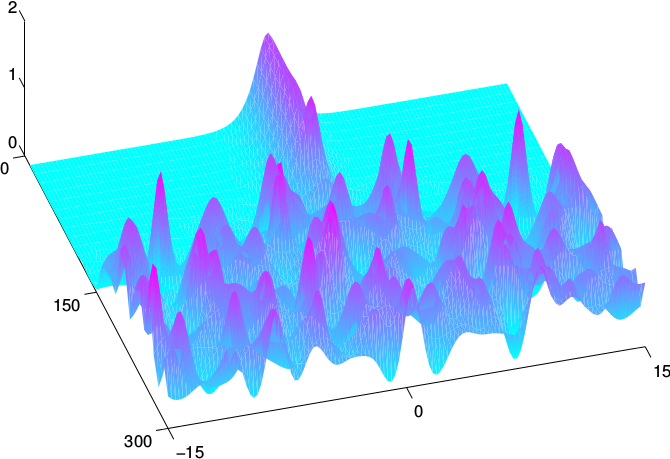
One line of our research concerns localized patterns on thesurface of a ferrofluid. Another area includes two-dimensionalsolitons in photonic crystals. We are traditionally active in the studies of the directly and parametrically driven damped non-linear Schrödinger equation; our work here is centred on the travelling and oscillating solitons and their complexes. Currently, the most active applications of these studies are to the ultrashort pulse syntheses in optical microresonators. In the frequency domain the single-soliton states correspond to low-noise optical frequency combs with smooth spectral envelopes, critical for broadband spectroscopy, telecommunications, astronomy and low noise microwave generation.

 

String theory

String theory is the leading program to combine both gravity and quantum mechanics into one consistent and unified framework. Over the past two decades we have discovered enormous riches both from the physics as well as mathematics perspectives within the framework of string theory. As members of the CTMP within the Laboratory for Quantum Gravity and Strings (QGaSLab) we are interested in both understanding the structure of string theory, discovering more about the properties of its basic, and not so basic ingredients, as well as using it as a tool to understand the world around us. The holographic principle, a direct consequence of the mathematical properties of string theory, allows us to study otherwise intractable problems which are extremely important to understand in a number of experiments within a particle physics context as well as table-top experiments within a condensed matter setting. Mysteries regarding the nature of high temperature superconductors, the nature of how quarks are confined within the centres of protons and neutrons, the nature of the quark-gluon plasma, and much more besides have been studied by international teams over the past two decades. Another aspect of our work focuses on investigating the properties of space and time using string and information theoretic mathematical methods. The topic of emergent space-time is being seen more and more as one of the most promising frontiers of string theory and there is much that we are finding about how space and time can be encoded in theories where the space we see around us is not a fundamental ingredient from the beginning but emerges from the dynamics of the theory. We have collaborations with well over 50 internationally renowned researchers in dozens of institutes around the world and we continue to attract world-class visitors.