Anisotropic numerical potentials for coarse-grained modeling from high-speed multidimensional lookup table and interpolation algorithms

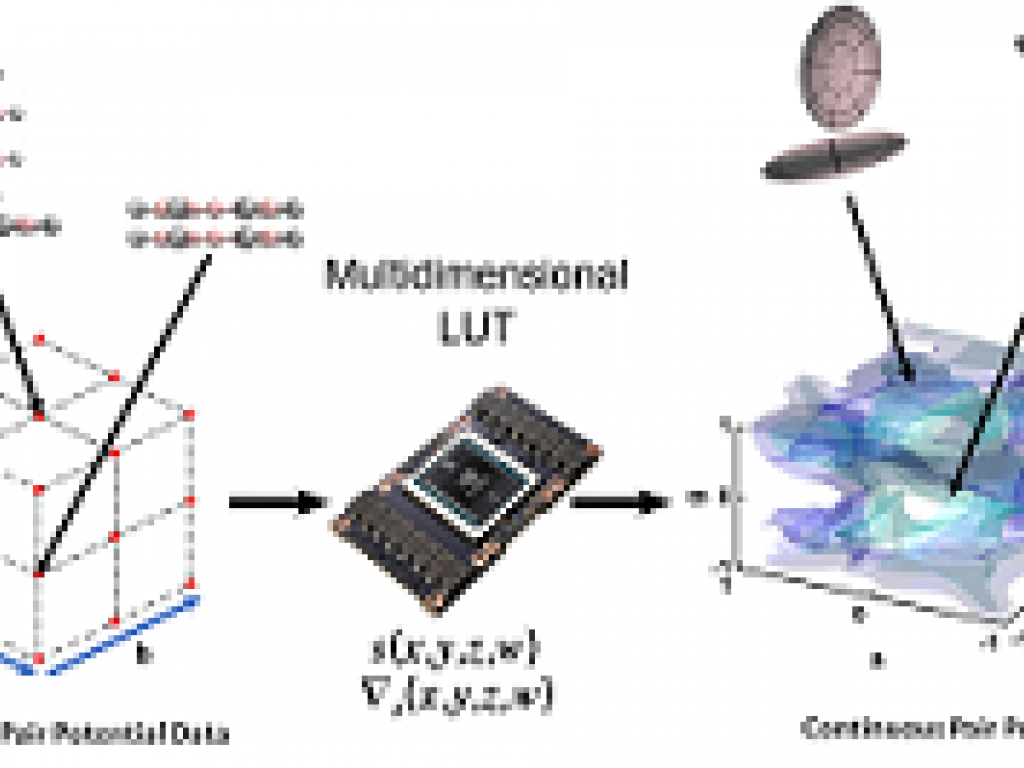
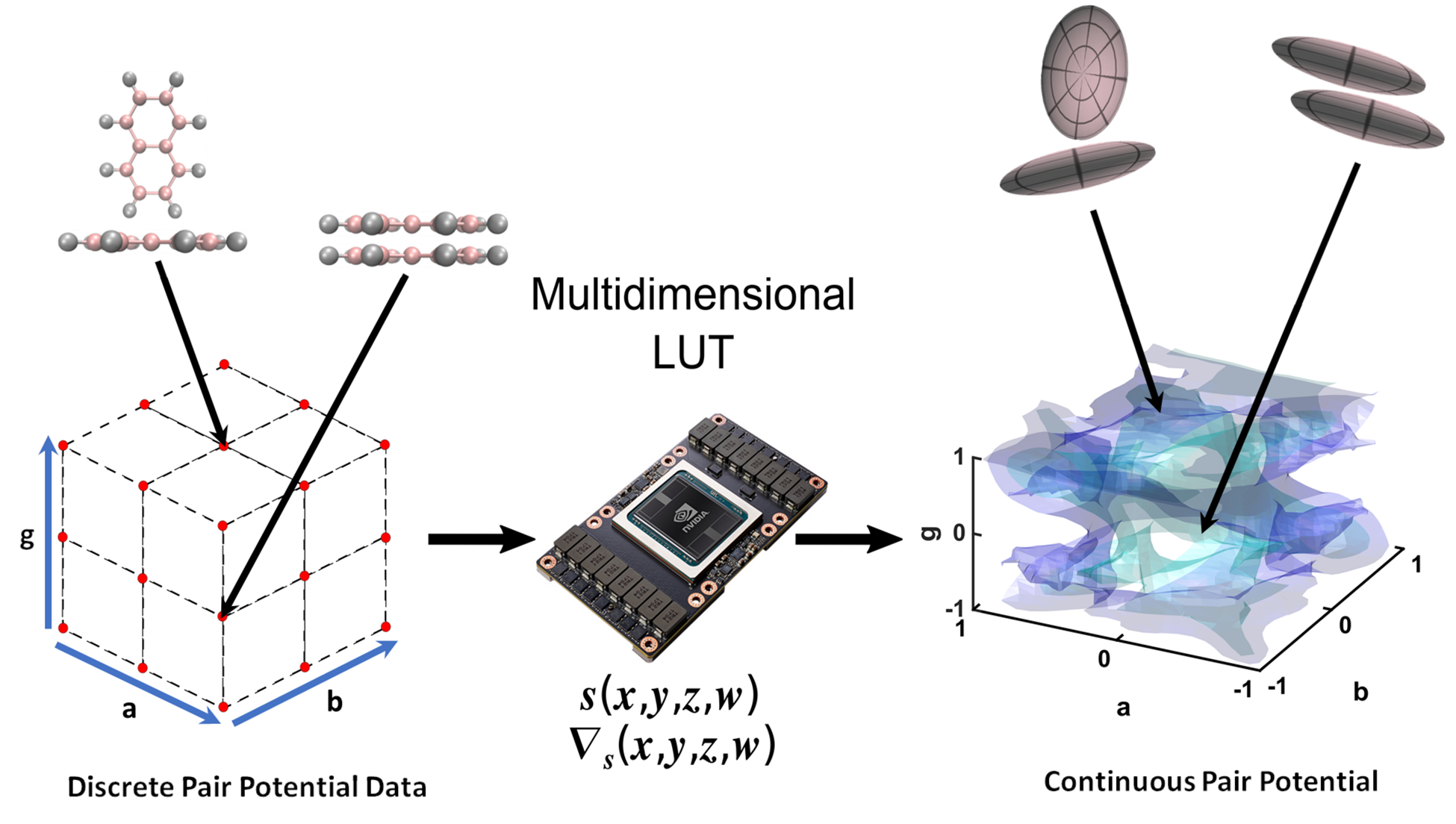
Earlier this year, the Journal of Computational Chemistry published the paper reporting the first GPU accelerated coarse-grain numerical potential algorithm authored by Ananya Gangopadhyay, Simon Winberg and Kevin J. Naidoo. The paper titled ‘Anisotropic numerical potentials for coarse-grained modelling from high-speed multidimensional lookup table and interpolation algorithms’ reports on a new method for increasing the accuracy in classical molecular dynamics simulations of anisotropic systems that opens the way to produce accurate coarse grain potentials for MD simulations. This accuracy is made possible by a high-speed numerical potential which delivers computational performance comparable with complex coarse-grained analytic potentials which, in turn, enables improved physical and chemical accuracy.

The key technological innovation came from the development of a high-speed Lookup Table (LUT) of four-dimensional gridded data that uses cubic B-spline interpolations to derive off-grid values and their associated partial derivatives. This method has high accuracy. The coarse-grained numerical potential (derived from interpolation of a uniaxial Gay–Berne (GB) potential using the LUT) has a 3% margin of error, while its partial derivates have a 5% margin of error. This method of using numerical potential based on a direct lookup of the atomistic potential landscape has the possibility to make for a more accurate anisotropic system coarse-grain modelling by significantly improving coarse-grain dynamics of complex molecules such as proteins.

Gangopadhyay, A, Winberg, S, Naidoo, KJ. Anisotropic numerical potentials for coarse-grained modeling from high-speed multidimensional lookup table and interpolation algorithms. J Comput Chem. 2021; 42: 666– 675. https://doi.org/10.1002/jcc.26487