A random collection of problems, quizzes and questions from Maths Digest. For even more, see the Archive.
Give yourself twenty minutes to solve the ten problems below.
1. 0.002 - 8 is equal to:
- 7.998
- -8.002
- 8.002
- -7.998
- -7.98
2. Which of the following numbers is closest to 37% of 85?
- 10
- 30
- 40
- 50
- 70
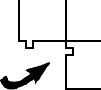
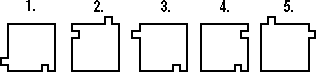
3. Which of the pieces fits into the space shown?
4. All 550 pupils in a school are going on an outing by bus. A bus can carry 64 pupils. How many buses are needed?
- 8
- 8.59375
- 8.6
- 9
- 10
5. In the diagram, the value of x is:
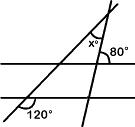
- 20
- 30
- 40
- 60
- 70
6. The positive integers are written in rows:
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| ... | ... | ... | ... | ... |
The row which has a sum nearest in value to 150 is the:
- 5th
- 6th
- 7th
- 8th
- 26th
7. A piece of paper containing six joined squares labelled as shown in the diagram is folded along the edges to form a cube. The label on the face opposite the X is:

- Z
- U
- V
- W
- Y
8. If 10025 - 25 is expressed as an integer, the sum of the digits is
- 219
- 444
- 432
- 453
- 435
9. A butcher sells a large number of braaivleis packs, each containing ten items: 4 chops and 6 sausages. At the end of the day he has sold altogether C chops and S sausages. Which of the following equations is correct?
- S+C=10
- 4C = 6S
- 4S = 6C
- 4S + 6C = 10
- 4C + 6S = 10
10. The diagram shows a house built of dominoes. The house has four stories and uses 24 dominoes. How many dominoes are needed to build a house with 70 stories?
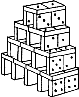
- 141
- 4899
- 5040
- 5041
- 2484
Below are seven quotations on the subject of logical argument, made by seven different writers: Lewis Carroll, T H Huxley, Samuel Johnson, John Keats, Omar Khayyam, Rudyard Kipling and Monty Python. Can you match the quotations with the authors? And which of the authors were also mathematicians?
- 'An argument is a connected series of statements to establish a proposition.'
- 'If it was so, it might be; and if it were so, it would be: but as it isn't, it aint. That's logic'
- 'Very rarely will he squarely push the logic of a fact
To its ultimate conclusion in unmitigated act' - 'Sir, I have found you an argument; but I am not obliged to find you an understanding'
- 'The Grape that can with Logic Absolute
The Two-and-Seventy jarring sects confute' - 'Logical consequences are the scarecrows of fools and beacons of wise men'
- 'Axioms in philosophy are not axioms until they are proved upon our pulses.'
"And what was he?
Forsooth, a great arithmetician."
This line comes from the first scene of the first act of one of Shakespeare's great tragedies. Which one?
Click for answer
Othello, Moor of Venice
The number 139854276 contains all the digits from 1 to 9, and is a perfect square:
118262
What other nine-digit numbers, with all their digits different, are squares? (The use of a computer is NOT regarded as cheating to solve this problem!)
Click to see the answer
Answer: There are 30 different nine-digit squares containing all the digits from 1 to 9, starting with 118262 = 139854276 and ending with 303842 = 923187456.
- Pieter Holtzhausen of Hoërskool Stellenbosch wins a R20 prize voucher for his solution using a program written in Turbo Pascal
152843769
157326849
215384976
245893761
254817369
326597184
361874529
375468129
382945761
385297641
412739856
523814769
529874361
537219684
549386721
587432169
589324176
597362481
615387249
627953481
653927184
672935481
697435281
714653289
735982641
743816529
842973156
847159236
923187456
Any rational number can be expressed as a repeating decimal. The length of the repeating segment is called the period of the decimal. So 1/7 = 0.142857142857... has period 6, while 1/11 = 0.9090909... has period 2.
What prime numbers have reciprocals with period five or less? This problem can be tackled crudely with a computer, but a technology-free solution is also possible.
Click to see the answer
We first note that 2 and 5 are the only prime numbers with terminating decimal expansions.
If p is prime and 1/p has period k, then
1/p = 10-kA + 10-2kA + ...
where A is a k-digit number. So:
1/p = 10-kA (1 + 10-k + (10-k)2 + ...)
= 10-k A / (1-10-k) (summing the geometric series)
= A / (10k - 1)
Therefore pA = 10k-1, and hence p is a prime divisor of 10k-1.
- if k = 1, p is a divisor of 9 = 32
- if k = 2, p is a divisor of 99 = 32× 11
- if k = 3, p is a divisor of 999 = 33 × 37
- if k = 4, p is a divisor of 9999 = 32 × 11 × 101
- if k = 5, p is a divisor of 99999 = 32 × 41 × 271
Thus the only possible values of p which give a reciprocal with period of five or less are 3, 11, 37, 41, 101 and 271.
- Rainer Hoft of Groote Schuur High School wins the R20 prize voucher.
The roads are all straight and level on the plains of Oblivia. Some distances in kilometers are given in the guide:
| Whair | Foggott | Urr | |
|---|---|---|---|
| Gawn | 225 | 540 | 1296 |
| Whair | 0 | 585 | 1521 |
How far is it from Fogott to Urr?
Click to see the answer
A rough sketch shows that Whair, Gawn and Urr lie in a straight line, since 225 + 1296 = 1521.
A more careful sketch suggests that angle FGW = 90 degrees, which can be confirmed since
5852 = 5402 + 2252
(Converse of the Theorem of Pythagoras).
It follows that FU2 = 5402 + 12062, so FU = 1404.
- The winner of the R20 prize voucher is Tiaan Towsen (Hoeërskool Brackenfell)
The following problem is from an examination paper from a Cape Town school. It turned out to be much more tricky than intended!
Find and sketch the locus of P such that the distance from P to the line y=1 is 3 less than its distance from the origin.
Click to see the answer
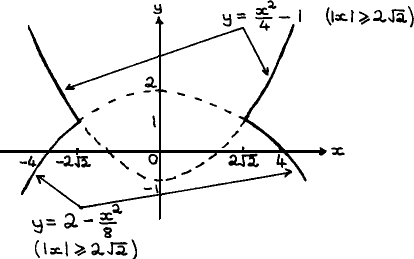
Bruce Merry (Westerford High School) wins a R10 prize voucher
Unit Shift
Find a number which is multiplied by 2 when you shift the units digit to the other end of the number.
Langford Sequences
The numbers 1, 1, 2, 2, 3, 3, ... n, n are to be arranged in a sequence in such a way that for each r = 1, 2, ... n, the two r's are separated by exactly r places. An example, with n = 4, is:
4 1 3 1 2 4 3 2
Such a sequence is called a Langford Sequence (see The Mathematical Gazette (1958) p.228).
Find a Langford Sequence with n = 8.
Problem of the Year
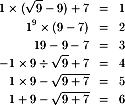
Can you continue this list, expressing 7, 8, 9 etc in a similar way? The rules of the game are that you must use all the digits 1,9,9 and 7 in that order, and the symbols +, -, ×, ÷, square roots and brackets.
Any of the Above?
Exactly one of the following five statements is true. Which one?
- All of the following
- None of the following
- Some of the following
- All of the above
- None of the above
Four Squares
Find four perfect squares, two consisting of three digits, one of two digits, and one of one digit, using each of the numbers 1,2,3,...,9 just once.
All Change
There are nine coins in South African currency:
1c, 2c, 5c, 10c, 20c, 50c, R1, R2, R5
Combinations of these coins cover all transactions, either by direct payment or by payment involving change.
For example, an item costing R1.98 can be paid with seven coins:
R1 + 50c + 20c + 20c + 5c + 2c + 1c
or by a transaction involving only two coins: a payment of R2 and 2c change.
Of all amounts under R10, which involves the largest number of coins, either as direct payment or one involving change?
Problems: Prime reciprocals
Any rational number can be expressed as a repeating decimal. The length of the repeating segment is called the period of the decimal. So 1/7 = 0.142857142857... has period 6, while 1/11 = 0.9090909... has period 2.
What prime numbers have reciprocals with period five or less? This problem can be tackled crudely with a computer, but a technology-free solution is also possible.
Swedish Problem
The following problem appeared in the Swedish magazine Elementa 4(95):
Visa att radien till den inskrivna cirkeln hos en pythagoreisk triangel (= en rätvinklig triangel med hetalssidor) är hetalsvärd.
Can you solve it?
From Foggott to Urr
The roads are all straight and level on the plains of Oblivia. Some distances in kilometers are given in the guide:
| Whair | Foggott | Urr | |
|---|---|---|---|
| Gawn | 225 | 540 | 1296 |
| Whair | 0 | 585 | 1521 |
How far is it from Fogott to Urr?
German Alphametric
Z W E I + D R E I --------- F Ü N F
Can you replace the letters by the digits 1,2,3,...,9 to make the addition correct? Each letter stands for a different digit.
Fivefold Flip
Seven coins are placed in a circle, with heads up. A move consists of flipping five coins in a row. Using only this move, can you make all the coins show tails simultaneously? What is the smallest number of moves needed?
How many pairs of supplementary angles can be found in the diagram below?
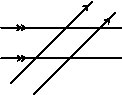
- Submitted by Lucas Motaung, Hartswater
Prove that the circumcircles of triangles OAB, OBC and OCA, where O is the orthocenter of triangle ABC, have the same radius.
- Submitted by Prof Poobhalan Pillay, University of Durban-Westville.
Prove that the fourth power of an even number which does not end in a zero, ends in a six.
- Submitted by Louis Brewis, De Kuilen High School
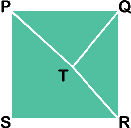
In the figure, PQRS is a square and T is a point inside the square such that PT=5, QT=4 and RT=1. Find the area of the square.
- Submitted by Mundia Mubyana, Pretoria Boys' High School
A farmer had 14 cows and three perfectly logical sons. On his deathbed he divided the cows so that all had some, the eldest had more than the middle who had more than the youngest. He told each son secretly how many he was to get. Then in front of all he asked the eldest if he knew how many the others had. The answer was 'No'. Then he asked the middle son the same question. Again the answer was 'No'. Then he asked the youngest son, and yet again the answer was 'No'.
Starting again, the old man asked the eldest son if he knew how many cows each of them was to get, and again the answer was 'No'. But when he asked the middle son, the answer was 'Yes'.
How many cows did each of the sons get?
- Submitted by Biddy Greene of the Unversity of Cape Town
